Usecases of importance sampling and scoring in Geant4

Michael Dressel

Table of Contents

1. Introduction

2. Mass-geometry

2.1. Particle suffers multiple scattering
2.2. Parent particle suffers process on mass-boundary
2.3. Daughter created by a physics process on boundary
2.4. Daughter created by biasing

3. Parallel-geometry

3.1. Particle suffers multiple scattering.
3.2. Particle suffers physics process on boundary
3.3. Daughter created by a physics process on a boundary
3.4. Daughter created by biasing

4. To the problematic usecases

5. Summary

Chapter 1. Introduction

This document should provide a list of usecases to check the behaviour of importance sampling and scoring against. A distinction is made between sampling in a mass and parallel geometry.

Chapter 2 and Chapter 3 give detailed usecase descriptions.

Chapter 4 sum's up the problematic usecases and their possible solutions.

Chapter 5 contains the summary.

Chapter 2. Mass-geometry

Table of Contents

2.1. Particle suffers multiple scattering
2.2. Parent particle suffers process on mass-boundary
2.3. Daughter created by a physics process on boundary
2.4. Daughter created by biasing

2.1. Particle suffers multiple scattering

Description:

A particle step reaches a boundary between volume A and B of the mass geometry and it's momentum is changed by a multiple scattering process.

Relevance:

Multiple scatteing applies for charged particles. The current version is not intended to be used for charged particles but future versions will.

Figure:

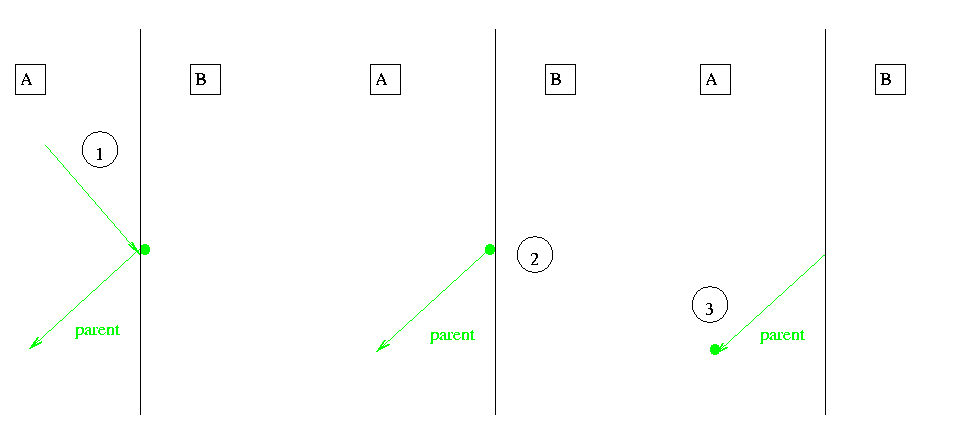
A particle crosses the boundary in the mass geometry. The momentum is changed by multiple scattering.

Detailed description:

Three steps 1, 2, 3 occur:

'st step:
1. Step one is limited by the transportation. The transportation moves the particle on the boundary and locates it in volume B.
2. Biasing split's or deletes the particle and changes weight correctly. See also: Section 2.4
3. Scoring counts the track as entering volume B
4. Multiple scattering changes the momentum to point back in volume A again.
'nd step:
1. Transportation limits step. Transportation locates particle in volume A.
2. Biasing split's or deletes the particle and changes weight correctly. See also: Section 2.4
3. Scoring counts the track as entering volume A
'rd step:
Step may be limited by any process.
Transportation locates particle at the new position

Comment:

Multiple scattering is related to volume A therefore the following should be considered:

Importance sampling should neither run in the first nor in the second step.
The particle should not be scored as entering volume B in the first step and it should not be scored as entering A in the second step.

2.2. Parent particle suffers process on mass-boundary

Description:

A particle step reaches a boundary between volume A and B of the mass geometry. It is located in volume B. Then a process returns a zero step length, get's called and changes the momentum back to A.

Relevance:

A process should never return step length = 0. But the situation applies also if a process proposes a step length so small that the track is located within a distance of kCarTolerance to the boundary.

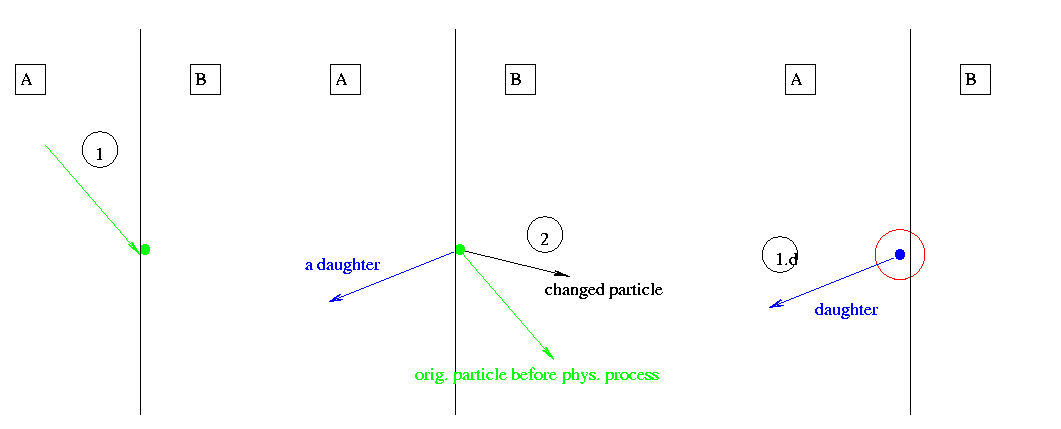
Figure:

Parent particle suffers a process on mass-boundary

A particle crosses the boundary in the mass geometry. The momentum is changed by a process that returned sl=0.

Detailed description:

Three steps 1, 2, 3 occur:

step
1. Step one is limited by the transportation. The transportation moves the particle on the boundary and locates it in volume B.
2. Biasing split's or deletes the particle and changes weight correctly. See also: Section 2.4
3. Scoring counts the track as entering volume B
step
1. A process returns step length = 0.
2. Scoring may count a collision with the correct weight according to volume B.
3. The process changes the particles momentum, and may create daughter particles. (See Section 2.3)
step
1. The step is limited by transportation. Transportation locates the particle in volumeA.
2. Biasing may delete the particle and change weight.
3. Scoring counts the track as entering volume A

Comment:

This way the particle is treated correctly.

2.3. Daughter created by a physics process on boundary

Description:

A particle step reaches a boundary in the mass geometry between volume A and volume B. A physical process returns steplength =0 and creates a daughter.

Relevance:

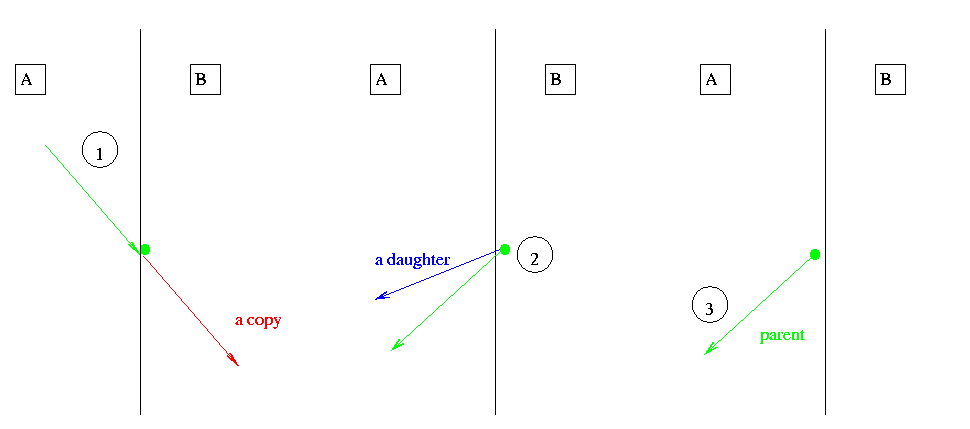
Figure:

A process creates a daughter on the boundary.

Detailed description:

The description of two steps of the particle and the first step of the daughter created by a physical process on the boundary:

Cross boundary.
This is equivalent to step one in Section 2.2
Physics process.
1. A physics process returns step length = 0.
2. Scoring may count collsision with the original track momentum and the correct weight.
3. The physics process changes the momentum of the particle and creates a daughter with momentum pointing to volume A.
First step 1.d of daughter
The daughter should be located in volume B inspide of having it's momentum pointing to volume A !
In this mass geometry case it should be done correct by the transportation since the Touchable of the doughter can be taken into account for location.

Comment:

If the daughter particle is located in volume B the situation should be treated correctly.

2.4. Daughter created by biasing

Description:

A parent particle crosses the boundary in the mass geometry. Biasing creates copies of the particle.

Relevance:

The most likely situation if a particle corsses a boundary and the importance of the enterung volume is higher then the importance of the exitiong volume.

Figure:

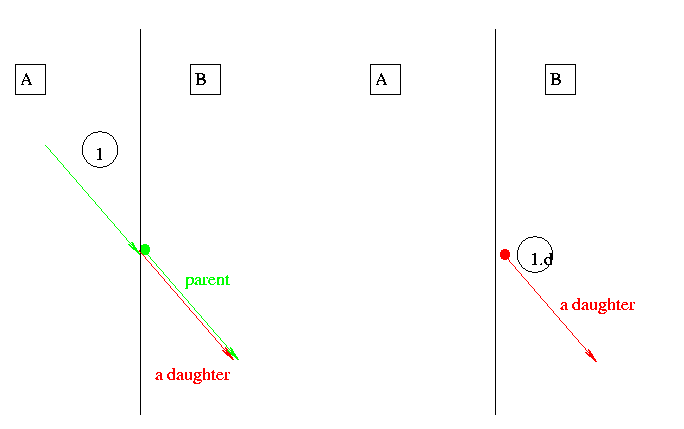
A particle crosses the boundary in the mass geometry. Biasing creates a daughter.

Detailed description:

A step 1 of the parent and the first step 1.d are shown:

parent step
1. Step one is limited by the transportation. The transportation moves the particle on the boundary and locates it in volume B.
2. Biasing split's or deletes the particle and changes weight correctly.
3. Scoring counts the track as entering volume B
1.d: first step of daughter
1. G4 locates the daughter in B.
2. Any process may limit the step.

Comment:

This should be the coorect treatment of the daughter particle created by importance sampling.

Chapter 3. Parallel-geometry

Table of Contents

3.1. Particle suffers multiple scattering.
3.2. Particle suffers physics process on boundary
3.3. Daughter created by a physics process on a boundary
3.4. Daughter created by biasing

3.1. Particle suffers multiple scattering.

Description:

A particle step is limited by a boundary in the parallel geometry between volumes A and B. Multiple scattering occures.

Relevance:

Multiple scatteing applies for charged particles. The current version is not intended to be used for charged particles but future versions will.

Figure:

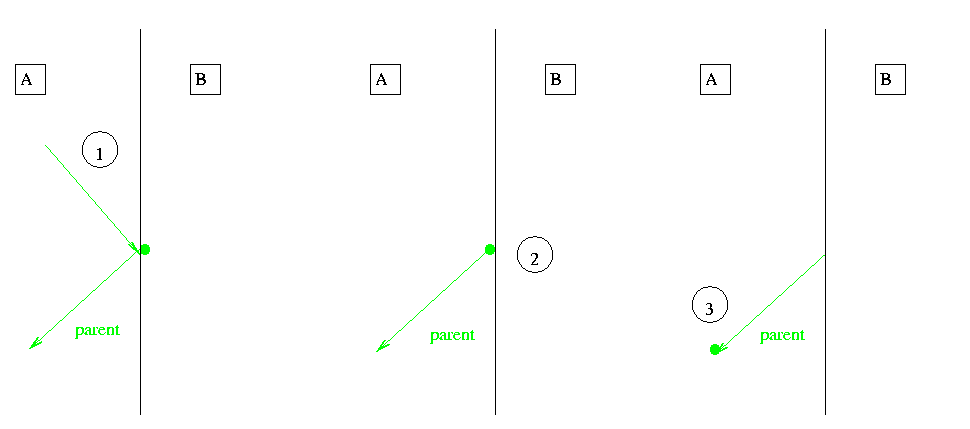
A particle crosses the boundary in the parallel geometry. The momentum is changed by multiple scattering.

Detailed description:

Three steps 1, 2, 3 occur:

Step:
1. The step is limited by a boundary in the parallel geometry found by the ParallelImportanceProcess.
2. Transportation moves the particle in the mass geometry.
3. The ParallelImportanceProcess moves the particle on the boundary and locates it in volume B of the parallel geometry. Biasing splits or plays Russian Roulette and changes the weight.
  The ParallelImportanceProcess may create daughters see Section 3.4
4. Scoring counts a track entering.
5. Multiple scattering changes the momentum of the particle.
Step:
1. The step is limited by the boundary in the parallel geometry found by the ParallelImportanceProcess.
2. Biasing split's or deletes the particle and changes weight correctly.
3. Scoring counts the track as entering volume A
Step:
The step may be limited by any process.
Transportation locates particle at the new position

Comment:

See the comment in Section 2.1.

3.2. Particle suffers physics process on boundary

Description:

A particle step is limited by a boundary in the parallel geometry between volumes A and B. A physics process returns step length = 0.

Relevance:

See Section 2.2.

Figure:

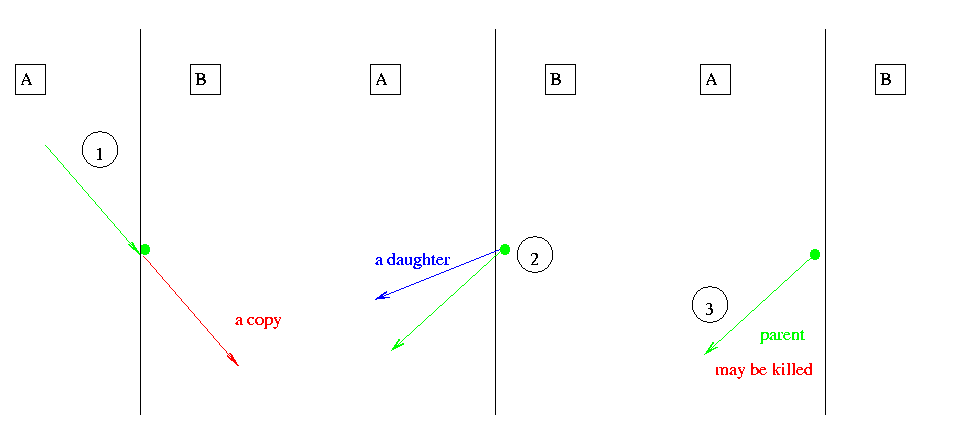
A parent particle crosses the boundary in the parallel geometry. A physics process happens on the boundary.

Detailed description:

Three steps 1, 2, 3 occur:

Step:
1. The step is limited by a boundary in the parallel geometry found by the ParallelImportanceProcess.
2. Transportation moves the particle in the mass geometry.
3. The ParallelImportanceProcess moves the particle on the boundary and locates it in volume B of the parallel geometry. Biasing splits or plays Russian Roulette and changes the weight.
  The ParallelImportanceProcess may create daughters see Section 3.4
4. Scoring counts a track entering.
Step:
1. A physics process retruns step length = 0.
2. Scoring counts a collision in volume B
3. The physics process changes the momentum of the particle and creates a daughter (See Section 3.3). Both momentums point towards volume A.
Step:
1. The ParallelImportanceProcess limits the step.
2. The ParallelImportanceProcess locates it in volume A of the parallel geometry. Biasing splits or plays Russian Roulette and changes the weight.
  The ParallelImportanceProcess may create daughters see Section 3.4
3. Scoring counts a track entering volume A.

Comment:

This way should be correct.

3.3. Daughter created by a physics process on a boundary

Description:

A particle step reaches a boundary in the parallel geometry between volume A and volume B. A physical process returns steplength =0 and creates a daughter.

Relevance:

See Section 2.3.

Figure:

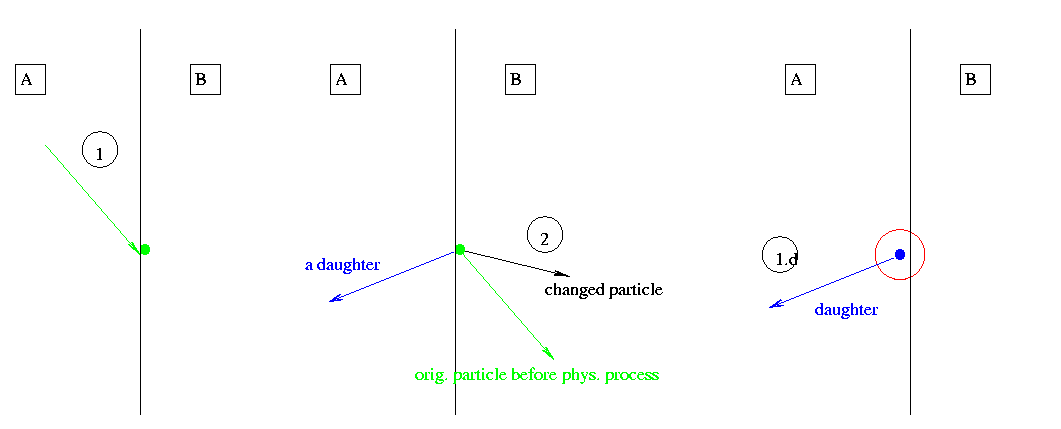
A process creates a daughter on the boundary.

Detailed description:

The description of two steps of the particle and the first step of the daughter created by a physical process on the boundary:

Cross boundary.
This is equivalent to step one in Section 3.2
Physics process.
1. A physics process returns step length = 0.
2. Scoring may count collsision with the original track momentum and the correct weight.
3. The physics process changes the momentum of the particle and creates a daughter with momentum pointing to volume A.
First step 1.d of daughter
According to the momentum the daughter is located in volume A .
The ParallelImportanceProcess does not occur. Therefore no biasing is applied and the weight is not changed!
Scoring counts a collision in volume A with the wrong weight.

Comment:

Locating the daughter particle in volume A is wrong.

3.4. Daughter created by biasing

Description:

A parent particle crosses the boundary in the parallel geometry. Biasing creates copies of the particle.

Relevance:

See Section 2.4.

Figure:

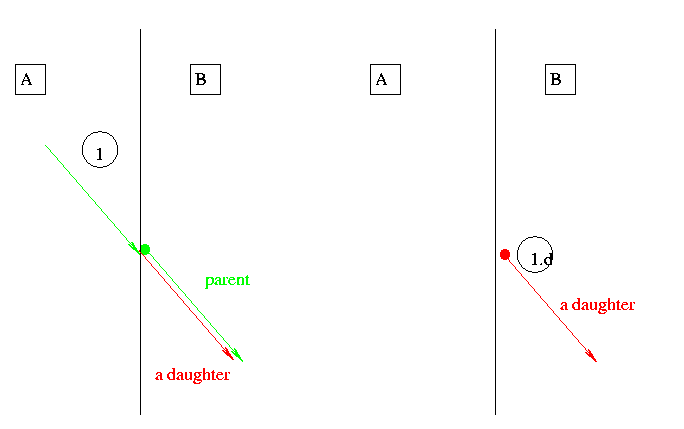
A particle crosses the boundary in the parallel geometry. Biasing creates copies.

Detailed description:

A step 1 of the parent and the first step 1.d are shown:

Step
1. Step one is limited by a boundary in the parallel geometry found by ParallelImportanceProcess. The ParallelImportanceProcess moves the particle on the boundary and locates it in volume B.
2. Biasing split's or deletes the particle and changes weight correctly.
3. Scoring counts the track as entering volume B
1.d: first step of daughter
1. The ParallelImportanceProcess locates the daughter in B.
2. Any process may limit the step.

Comment:

This should be the correct way.

Chapter 4. To the problematic usecases

Of this (probably incomplete) list of usecases the cases Section 2.1, Section 3.1 and Section 3.3 are treated wrongly. The first two cases apply to charged particles only. The other usecase applies for the parallel geometry. Therefore this documents does not contain problematic usecases for neutral particles in the mass geometry.

The only wrongly treated usecase in this document applying also for neutral particles is Section 3.3.

The reason for the problem is: In contrast to the mass geometry cases there is no information about the current Touchable in the parallel geometry related to a newly starting particle.

The two types of particles starting on a parallel boundary are:

Section 3.3 particles created by a physical process on the boundary.
Section 3.4 particles created by importance sampling. All particles created by importance sampling start on a boundary.

The particles starting on the boundary may be located in either of both volumes depending on the geometry e.g. which volume is deepest.

In order to treat the much more frequent cases of type number 2. correct it has been chosen to take the direction of the particle momentum into account. But this treats the cases of type 1. wrong.

To solve this problem it has been considered to somehow provide the information about the Touchable in the parallel geometry. It is not clear "who" should give that information to "whom". While the importance sampling process knows about the parallel geometry and therefore could assign a touchable to the particle in principle, the physics processes can't do that.

Chapter 5. Summary

This document gives a list of usecases which should be considered for the implementation of importance sampling and scoring.

When changing the behaviour of importance sampling the resulting algorithm should be checked at least against the usecases listed here.

The current problem to be solved is to treat the usecase Section 3.3 right without messing up usecase Section 3.4 .